Maths teachers are often accused of taking a reductionist approach to teaching; turning the curriculum into a set of rules and procedures that simply need to be memorised, with constant drilling and testing to ensure performance.

And whilst there is (in my opinion, at least) a place for memorising content, and for drills and for testing, this isn’t and can’t be all that our subject is.

Maths is about big ideas. Ideas like addition, comparison, equality, fraction and, even, number.

Quick read: Could this be the answer to the Stem teacher shortage?

Long read: The GCSE - is it a reliable measure of education?

Quick listen: The specific benefits of generalising about maths

Want to know more? ‘Let’s take maths anxiety out of the equation’

These ideas grow and develop as they meet each other and then pull away to meet other ideas. And out of them comes our subject; every procedure, every fact, every calculation, every result.

Big mathematical ideas

But big ideas cannot be taught in one go. They cannot even be taught to completion in sequence.

Consider the ideas of addition and multiplication. Multiplication derives from addition - as the repeated addition of the same value.

But multiplication doesn’t stop there. It takes on new meanings and interpretations. One of the ways of seeing multiplication is about changing the counting unit.

For example, 4 × 5 can be seen as having four items that are worth 5; think of how much money four £5 notes are worth.

But if we change the counting unit, we can then think about adding these new units. If we have four £5 notes, and then we get three more, the result is we have seven £5 notes. We are showing here that 4 × 5 + 3 × 5 = 7 × 5.

So, multiplication comes back to addition and then moves away again. Eventually, multiplication then links to area, and from there to squares and square roots. Which we then see come back to addition again when we consider questions like 4√5 + 3√5.

The result is this paradoxical situation where we need to understand addition to understand multiplication, but then we need to understand multiplication to understand addition.

A puzzling paradox

So how do we resolve this paradox, and others like it? We highlight underlying structure in small bits.

Again, take the idea of addition. We might start in the earlier years of schooling by looking at calculations like 4 + 3. Teaching kids that this results in 7 is important, but what is more important is to teach them what is happening when we add.

How do we make sense of the idea of addition? Equally important here is that learners see not just one way of making sense of this, but multiple ways (although perhaps not all at once!).

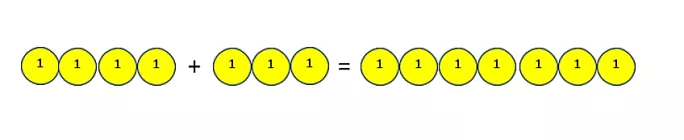
In particular, for addition, we might see this as the collecting of like objects, as per the image below:

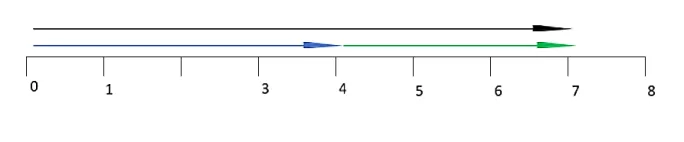
Alternatively, we might see addition as the connecting of different lengths:

These are just two possibilities - there are others. These help our learners to understand part of the shape of this big idea of addition, helping them to see the underlying structure.

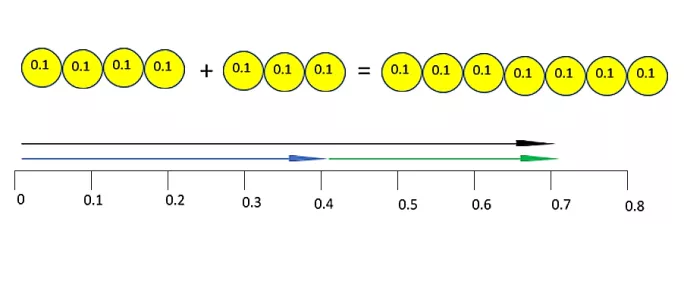
Armed with this understanding, it is now a small step to another part of this idea, perhaps the addition of decimal numbers:

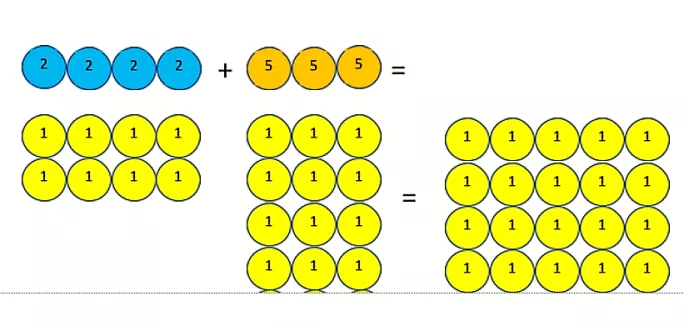
Or perhaps we can bring the idea of addition together with another two big ideas, equivalence and exchange:

These small steps around an idea, and the links with other ideas, are what allow learners to make more and more sense of the big idea, seeing its structure, seeing what remains true when other things change, seeing how ideas combine in a way that is understandable from the properties of each idea, and building an understanding of mathematics.

So, when you’re planning your lessons for next week, or next year, I urge you to move away from thinking about what process you are going to teach them today, or what fact they are going to learn.

Instead, focus on what mathematical ideas pupils will be working with, how you can let them make sense of these ideas and let them see the connections between these ideas.

Let them see that what they are working on is just a small step away from what they already understand about these big ideas.

Peter Mattock is head of maths at an 11-16 school in Leicestershire and author of Visible Maths