I’ve got a thing about success criteria. Very often, the line between what we want children to learn to do and the task that we ask them to carry out is blurred. The gap is perhaps most stark when it comes to problem-solving in maths.

In many classrooms the “read, underline, calculate, solve, answer, check” (RUCSAC) acronym, or something similar, will be plastered on the wall and used as success criteria for problem-solving.

However, I’d argue that RUCSAC does not present a valid set of criteria for such an important part of maths; rather it prevents children from learning to think mathematically. Here’s why:

Read 

What an unnecessary criterion. Of course, the teacher will model reading the problem and, of course, the child will read it too. It has been shoe-horned in to make a memorable acronym.

Underline 

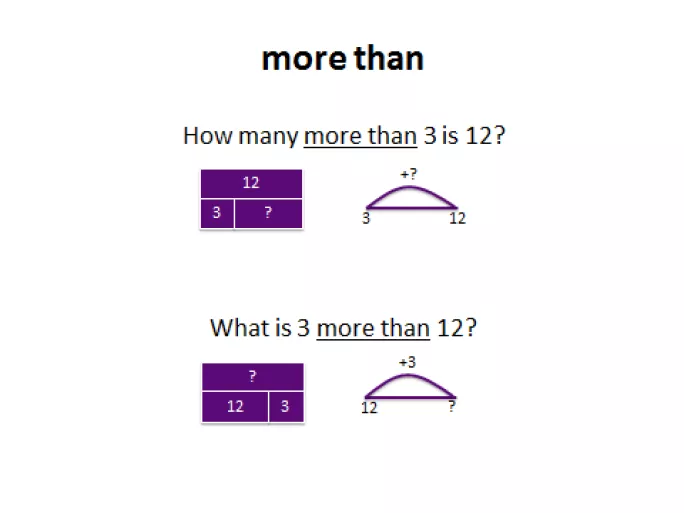
This can refer to underlining numbers or words. While it is important to pick out numbers, there are often superfluous quantities or amounts to distract the problem solver, so the important thing isn’t underlining them, but understanding the problem in its entirety. Similarly, although words unlock the meaning of the problem, it’s not as simple as a word equating an operation. For instance, if we teach children that the phrase “more than” always means that one must perform addition, we set them up for failure.

Calculate

There is a huge conceptual jump from underlining to calculating. It assumes that a child has already understood, whereas the crux of problem-solving is understanding what to do once you have figured out the meaning of the problem.

Solve 

Another unnecessary criterion. Once children have calculated what’s necessary, it should be an unsaid next step to solve the problem.

Answer 

Consider the child who does the working but never actually answers the question. I’d suggest that this is down to the child not fully understanding the problem, rather than belligerently leaving the problem unfinished.

Check 

A child can only check that an answer makes sense if they have understood the problem in the first place. It’s something that is desirable, but simply telling children to check their answer won’t necessarily result in success.

Picking apart a strategy like RUCSAC makes it clear that if we encourage surface-level thinking, we will only get surface-level learning. When it comes to solving problems, success comes not from applying a skill, but from using our memory. Most likely, we will figure out the underlying structure of the problem by recalling previously solved problems from memory.

Here’s my alternative. Instead of teaching that problem-solving is a skill, we should teach children the inherent ambiguity of vocabulary in different contexts, the underlying mathematical structures and common problem scenarios. When it comes to vocabulary, we must show children how a word or phrase can mean different unknowns.

For example:

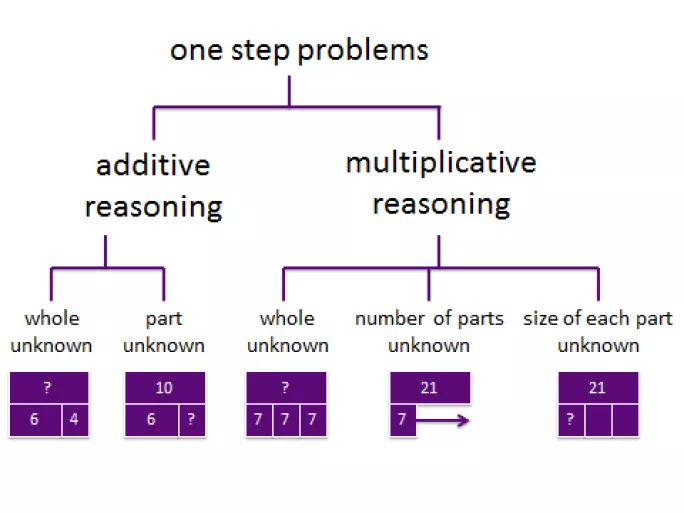
When teaching additive reasoning, any problem is either one where the whole is unknown or where one of the parts is unknown. For multiplicative reasoning, there are three underlying patterns, yielding five basic structures:

Most one-step maths problems will fit one of these five basic problem types and most multi-step problems are a combination of these. 

It is well within our reach to teach the vast majority of children what these underlying patterns are and how to identify them from an early age.

Identifying them is one thing; knowing what to do with the information is quite another. However, some basic rules can be applied for each unknown. For problems involving additive reasoning, here are my success criteria:

• Is the whole unknown or a part unknown?
• If the whole is unknown, add the parts.
• If a part is unknown, subtract the known part(s) from the whole.

These criteria will support teachers to model problem-solving based on sound mathematical thinking, as well as supporting children to look deeper than the contextual surface of problems. In time, the goal is that these criteria will become encoded in children’s long-term memories and that they can use this information to decide what to do when dealing with new problems.

The RUCSAC model is mathematically empty - a bag for the sake of having a bag. If we want to develop children’s mathematical thinking, it’s time to throw away that old RUCSAC.

Nick Hart is headteacher of Chalfont Valley E-ACT Primary Academy in Buckinghamshire