Slope Guided Notes
This resource includes:
different types of slopes
calculate slope from graphs, tables, pictures, and points
undefined and zero slopes. Also,
how to find a coordinate if given 1.5 points and the slope
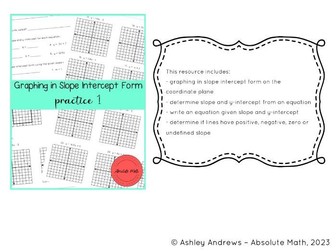
Graphing in Slope Intercept Form Guided Notes
This resource includes:
graphing in slope intercept form on the coordinate plane
determine slope and y-intercept from an equation
write an equation given slope and y-intercept
determine if lines have positive, negative, zero or undefined slope
undefined
Gradients - Treasure Hunt
16 gradients clues, including negatives, positives, undefined and zero on a variety of scales. Work out the answer then find the next clue that has that answer at the top.
Includes answer sheet and solutions.
Also includes a letter on each clue that form an anagram to be solved: gradients are cool.
logarithmic derivatives practice- derivative sign chart
logarithmic derivatives practice- derivative sign chart
this resource covers:
how to find inflection points on a derivative graph
first derivative and second derivative graph
second derivative at point of inflection
the second derivative be can undefined at an inflection point
SLOPE - FINDING SLOPE OF TWO POINTS COLORING ACTIVITY
This is a coloring activity on finding the slope of two points for 16 problems. Students will color the picture according to the correct answer for each problem. I used 8 colors in the design and I put in 2 different designs. The “A” design goes with the flower problems and the “B” problems go with the positive, negative, 0 and undefined sheet.
Deutsch Artikel- und Adjektivdeklination Typ 1-3 (German article and adjective alignment)
This resource / overview aids learners in learning, automating and applying the correct gender and case alignment for Nominative, Akkusative, Dative and Genitive.
The three article types are displayed along with the matching adjective ending, exceptions and additional rules.
Typ 1 defined articles + adjective endings
Typ 2 undefined articles + adjective endings
Typ 3 adjective endings without article
Improper Integrals - Further maths A level A2
Improper Integrals covers;
Identify why a given integral is improper
Understand and clearly demonstrate the limiting processes involved, using correct notation
Identify when and why an improper integral does not have a finite value
Identify the point(s) where the integrand is undefined
Evaluate improper integrals where the integrand is undefined at a value in between the limits of integration.
These PowerPoints form full lessons of work that together cover the full A level Further Maths course for the AQA exam board. Together all the PowerPoints include;
• A complete set of notes for students
• Model examples
• Probing questions to test understanding
• Class questions including answers
• Individual whiteboard work
• Links to exercises in ‘AQA approved textbooks by Camb uni Press’ these can easily be edited for your textbook
The PowerPoints can be used in the lesson and also given to students that have missed a lesson
Videos of the lessons are all on You Tube so you can see the PowerPoint lessons fully first
I have added ‘Further Maths 5 - Matrices Transformation’ and ‘Further Maths 23 - Network Flows’ for free download
Please leave a review as it will really help me to improve my resources
Unusual Equations (Index Laws)
You can use this in a number of ways.
I sometimes get the kids to solve by trial and error (good practice for substitution on a calculator). When they get an x that "works" I write it up on the board. With a board full of solutions I then ask them if they can find any patterns.
Alternatively you could insist that they use index laws to solve the equations in the first place.
Opportunities to discuss 1^n=1, n^0=1, (-1)^2n=1 and 0^0=undefined.
IB Math AI AHL 1.9 - Laws of Logarithms
IB Math HL AHL 1.9 – Laws of Logarithms
Topic: Number and Algebra
Level: IB Mathematics: Analysis and Approaches (HL)
File Type: Editable Slides / Worksheet
Overview
This resource extends students’ understanding of logarithmic properties and their relationship to exponents.
Students will explore the fundamental laws of logarithms, learn how to derive these relationships, and apply them to solve logarithmic and exponential equations.
The lesson provides both conceptual explanation and practical application, emphasizing the connection between algebraic manipulation and the structure of logarithmic expressions.
Learning Objectives
By the end of this lesson, students will be able to:
State and apply the laws of logarithms in simplifying expressions.
Derive logarithmic laws from the corresponding laws of exponents.
Solve logarithmic and exponential equations using algebraic reasoning.
Identify when logarithmic expressions are undefined based on domain restrictions.
Use logarithmic rules to evaluate and simplify complex expressions efficiently.
What’s Included
Summary table of the Laws of Logarithms with equations and corresponding names.
Step-by-step derivations explaining the logic behind each property.
Practice problems requiring students to apply the laws of logarithms to simplify or solve equations.
Worked solutions emphasizing correct domain restrictions (e.g., when logarithms are undefined).
Additional “Properties of Logs” examples that illustrate key concepts such as product, quotient, and power laws.
Topics Covered
Definition and properties of logarithmic functions.
Laws of logarithms: product, quotient, and power rules.
Connection between exponential and logarithmic equations.
Derivation of logarithmic properties from exponent laws.
Solving equations involving logarithmic expressions.
Domain and range considerations for logarithmic functions.
Why You’ll Love It
Builds directly on prior knowledge of exponents and logarithms from the SL course.
Encourages conceptual understanding through derivation, not just memorization.
Includes problem-solving tasks suitable for IB HL-level rigor.
Visually organized and ready for classroom instruction or digital teaching.
Aligned with the IB Math HL syllabus and designed for both teaching and review.
IB Math AI SL 5.1 - Limits
IB Math AI SL 5.1 – Limits
Topic: Calculus
Level: IB Mathematics: Applications and Interpretation (SL)
File Type: Editable Slides / Lesson Presentation
Overview
This resource introduces the concept of limits as the foundation of differential calculus.
Students learn how limits describe the behavior of functions as inputs approach specific values, and how this concept leads to the definition of the derivative as an instantaneous rate of change.
The lesson builds from intuitive examples to the formal definition of a limit, helping students understand the transition from average rate of change to instantaneous gradient through graphical and analytical reasoning.
Learning Objectives
By the end of this lesson, students will be able to:
Describe the concept of a limit intuitively and formally.
Recognize when a function is well-defined or undefined at specific points.
Use limits to describe the behavior of a function as ( x ) approaches a value.
Understand that the derivative is defined as a limit of the average rate of change.
Interpret the derivative as both the gradient of a curve and a rate of change.
What’s Included
Conceptual introduction showing functions that are well-defined and undefined at certain points.
Visual exploration of function behavior as ( x ) approaches a specific value.
Intuitive definition of a limit followed by the formal epsilon-delta definition
Examples illustrating how limits predict the behavior of functions near discontinuities.
Step-by-step transition from average rate of change (secant line) to instantaneous rate of change (tangent line).
Definition of the derivative as a limit
Comparison of gradient behavior for linear vs. nonlinear functions.
Topics Covered
Concept and definition of a limit.
Formal epsilon-delta definition.
Average vs. instantaneous rate of change.
Definition of the derivative as a limit.
Interpreting limits graphically and analytically.
Why You’ll Love It
Establishes a clear conceptual foundation for all of calculus.
Combines visual, numerical, and analytical approaches to limits.
Smoothly bridges intuitive understanding with formal mathematical definition.
Fully aligned with IB Math AI SL Topic 5: Calculus.
Classroom-ready and ideal for interactive instruction or student exploration.
Tags: IB Math SL, Limits, Derivatives, Gradient, Rate of Change, Continuity, Calculus Foundations, IB Curriculum, Lesson Slides
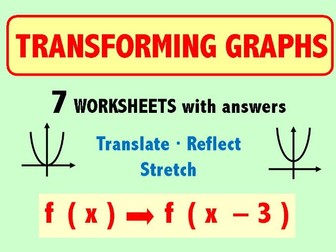
Transforming Graphs
Seven worksheets for exploring the effect of transformations on graphs.
Learn how parabolas and cubic graphs can be sketched quickly by looking at their equations and seeing how they are transformed from the basic y = x² and y = x³ graphs.
Transform graphs of undefined functions by looking at the graph’s new equation and deciding what transformation it represents. Translations, reflections, reflections and stretches.
These worksheets include answers and are suitable both for extra support for A-level students who need to be able to understand transformations fluently.
For more resources like this please visit the SKILLSHEETS Shop
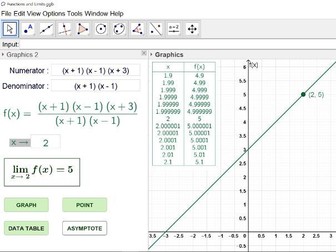
Functions & Limits (Geogebra)
This is a geogebra program for use as a visual aid when teaching students about limits as a prelude to differential calculus. This program has been designed using Geogebra 5.0 (download version). You simply enter the numerator and denominator expressions of a function and specify and x limit. The program will then graph the function and display a point that represents the function value as the x values approach the specified limit. If the function is unable to be evaluated at the limit, the program will advise that the function is undefined and will show this as a hole in the graph. The program can also present a table of values as the function approaches the limit as well as any asymptote lines that exist in the function.
VOCABULARY STORY 675 WHAT THINGS MADE LINCOLN A CLEAR PICK FOR PRESIDENT?
MAKE A STORY WITH THESE WORDS:
OBSCURE
RUDIMENTARY
STAGNANT
VIGOR
NEBULOUS
SUPERFLUOUS
RETICENT
CHARISMATIC
REVERENT
REPUDIATE
Lincoln came from Illinois, a rudimentary stagnant place in 1836.
He was obscure and nebulous; yet he had superfluous charm - a charismatic nature.
He had vigor to repudiate slavery which won him fame.
Never reticent, he had a clear path to the presidency.
In 1836, Lincoln hailed from a modest, unmoving corner of Illinois. Though largely unknown and undefined, he possessed an excess of charm and magnetic appeal. With fierce energy, he rejected slavery and rose to prominence. Bold and unwavering, his journey to the presidency was undeniable.
Daily Activities PowerPoint Presentation
Daily Activities PowerPoint Presentation-ESL Fun Games
Try out our Daily Activities PowerPoint Presentation.
Description:
Each Regular PowerPoint Slideshow has one topic with 6 task categories; What’s in the Photo? Answer the Question, True or False, Fill in the Blank, Multiple Choice and Spot the Error. Every PowerPoint Slideshow has a total of 60 different tasks with answers. All 120 slides are also animated with sounds!
How to Use It:
Open the slideshow in PowerPoint. Click the mouse or the right arrow button on your keyboard to advance to the next slide. To move back a slide, click the left arrow button. Students can take turns performing the tasks on the slides or present the slideshow to the entire class as a fun classroom activity or topic warmer.
Notes:
Use our worksheets, Jeopardy Game, Board and Card Games as complimentary activities for the PowerPoint Slideshow
undefined
IB Math AI Worksheet SL 5.6 - Local Maxima & Minima
This IB Maths AI SL 5.6 – Local Maxima & Minima resource develops students’ understanding of how derivatives are used to identify and classify turning points on curves. Learners focus on critical points, where the derivative is zero or undefined, and use both the first derivative test and second derivative test to determine whether these points represent local maxima or local minima. The material builds clear connections between algebraic derivative information and changes in graphical behaviour.
Structured tasks guide students through differentiating functions, solving (f’(x)=0), and constructing sign charts to interpret where functions increase or decrease. Students learn to recognise how sign changes in the derivative indicate turning points, and how concavity information from the second derivative supports classification. Conceptual prompts emphasise the difference between local and absolute extrema, reinforcing exam-relevant reasoning.
IB Math AI Worksheet 5.1 - Limits
This IB Maths AI SL 5.1 – Limits worksheet builds students’ foundational understanding of limits as a way of describing how functions behave as inputs approach particular values. Learners develop fluency with limit notation, one-sided limits, and the idea that a function can approach a value even when it is undefined at that point. Core concepts such as approaching values, discontinuities, and the connection between limits and rates of change are introduced through clear, structured tasks.
Guided activities move from estimating limits using tables and algebraic simplification to classifying removable, jump, and infinite discontinuities. Students practise evaluating one-sided limits, applying limit laws, and using factoring and rationalising techniques to resolve indeterminate forms. The resource also supports conceptual reasoning, encouraging learners to explain in words why limits exist or fail to exist and to interpret graphical and algebraic behaviour together.
IB Math AI 5.1 - Limits Notes
This IB Maths AI SL 5.1 – Limits, Rate of Change & Derivatives resource introduces the core ideas of calculus through clear, intuitive development. Students first explore limits as the value a function approaches near a point, even when the function may be undefined, building understanding of function behaviour at “problem points” .
The lesson then links gradients of lines to average rate of change on curves using secant lines, before introducing instantaneous rate of change and the derivative through the difference quotient and limit notation. Students learn to interpret the derivative as the gradient at a single point and become familiar with standard derivative notation .
Structured notes, guided examples, and an optional extension on the formal definition of limits support both core SL understanding and deeper conceptual insight, preparing students for further calculus applications in IB Mathematics AI SL.
(Note: The student + teacher notes are free! Thanks for your support. Consider purchasing the IB Math AI 5.1 - Limits PPT to supplement these. Feel free to share this link, and don’t forget to leave a 5-star review if you found these helpful.)