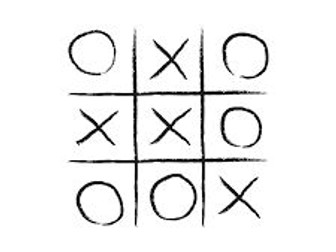
Tic-Tac-Toe (Noughts and Crosses) Investigation (Scaffolded)
This investigation looks at finding the number of winning lines on 2D and 3D tic-tac-toe grids. Students played the games first using the blank grids and then were given the investigation to work through. An extension activity would be to find the number of winning lines on a 4x4x4 grid.