Equations of motion
Applications of the four equations of motion, also known as suvat equations. Problems with hand written solutions.
A4: rigid body mechanics, Engineering mechanics, Torque, Rotational dynamics
the torque τ of a force about an axis as given by τ = Fr sin θ
• that bodies in rotational equilibrium have a resultant torque of zero
• that an unbalanced torque applied to an extended, rigid body will cause angular acceleration
• that the rotation of a body can be described in terms of angular displacement, angular velocity and
angular acceleration
• that equations of motion for uniform angular acceleration can be used to predict the body’s angular
position θ, angular displacement Δθ, angular speed ω and angular acceleration α,
that the moment of inertia I depends on the distribution of mass of an extended body about an axis of
rotation
• the moment of inertia for a system of point masses as given by I = Σmr2
• Newton’s second law for rotation as given by τ = Iα where τ is the average torque
• that an extended body rotating with an angular speed has an angular momentum L as given by
L = Iω
• that angular momentum remains constant unless the body is acted upon by a resultant torque
Bundle
A2 FORCES AND MOMENTUM IBDP PHYSICS
This resource is all in one package to teach or learn the concept of resultant forces .
It includes a detailed presentation covering FBD, net forces applying Newton’s first and second and second law
The resource is the second subsection A2 under IBDP theme A and also includes syllabus covering A levels and K12
It includes a PPT and worksheet created by me from past paper with ms attached.
It also includes my youtube video overing the same topic.
A3:Work, energy and power
the principle of the conservation of energy
• that work done by a force is equivalent to a transfer of energy
• that energy transfers can be represented on a Sankey diagram
• that work W done on a body by a constant force depends on the component of the force along the
line of displacement as given by W = Fs cos θ
• that work done by the resultant force on a system is equal to the change in the energy of the system
• that mechanical energy is the sum of kinetic energy, gravitational potential energy and elastic
potential energy
• that in the absence of frictional, resistive forces, the total mechanical energy of a system is conserved
• that if mechanical energy is conserved, work is the amount of energy transformed between different
forms of mechanical energy in a system
Sale
A1:Motion graphs and projectile motion
The resource includes tips and tricks to solve sums in projectile motion applying equations of motion.
IBDP physics theme A1. It covers Kinematics , equation of motion, projectile motion and motion graphs.
Complete resources for teachers and students.
undefined
Sale
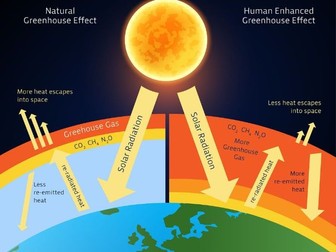
B2: GREEN HOUSE EFFECT
Conservation of energy
Emissivity, Albedo, Solar constant
Mean value of incoming Solar radiation is S/4
B1:Thermal energy transfer
molecular theory in solids, liquids and gases
•density ρ as given by ρ = mV
• that Kelvin and Celsius scales are used to express temperature
• that the change in temperature of a system is the same when expressed with the Kelvin or Celsius
that Kelvin temperature is a measure of the average kinetic energy of particles as given by Ek =
3
2
kBT
• that the internal energy of a system is the total intermolecular potential energy arising from the forces
between the molecules plus the total random kinetic energy of the molecules arising from their
random motion
• that temperature difference determines the direction of the resultant thermal energy transfer between
bodies
• that a phase change represents a change in particle behaviour arising from a change in energy at
constant temperature
• quantitative analysis of thermal energy transfers Q with the use of specific heat capacity c and specific
latent heat of fusion and vaporization of substances L as given by Q = mcΔT and Q = mL
• that conduction, convection and thermal radiation are the primary mechanisms for thermal energy
transfer
• conduction in terms of the difference in the kinetic energy of particles
• quantitative analysis of rate of thermal energy transfer by conduction in terms of the type of material
and cross-sectional area of the material and the temperature gradient as given by ΔQΔt= kAΔTΔx
• qualitative description of thermal energy transferred by convection due to fluid density differences
• quantitative analysis of energy transferred by radiation as a result of the emission of electromagnetic
waves from the surface of a body, which in the case of a black body can be modelled by the StefanBoltzmann law as given by L = σAT4
where L is the luminosity, A is the surface area and T is the
absolute temperature of the body