Vectors in geometry
Worksheet of basic vectors, incuding adding vectors, finding vectors with midpoints or ratios of a line. Used at beginning of topic to ensure students understand direction and working with vectors. Please make comments.

Coordinate Geometry
Midpoints, normals and tangents, circles.
Generated by Mathster.com under the Share-Alike license.

Geometry project - Making Straw Planes
**Students will need around 5 plastic straws each, paper, sticky tape and scissors**
A fully differentiated Geometry project on making optimum straw aeroplanes. Easy to carry it out in any way you wish. Can do it over 2 lessons or do it over 5. Three levels of difficulty are indicated by the colour of the straws in the slides.
Different difficulties assume different understanding of various topics.
Easy (green): Measurements, circumference (not calculating), area of rectangles, Mean
Medium (yellow): above plus area of circles and area of triangles
Hard (red): above plus volumes of cylinders and areas of trapeziums.
Recommended for 11 to 14 year olds at the end of the year.

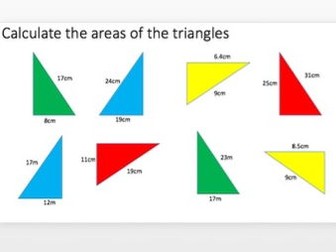
VOLUME of triangular Prisms - GEOMETRY - WITH ANSWERS
Excellent resource differentiated with 6 levels of differentiation on volume of Triangular prisms, working out the volume, working backwards to find missing lengths, and using volume of cuboids and triangular prisms in problem solving questions.
Can be used for any set as it has questions for the lower ability and the higher levels can stretch the higher ability.
Please do leave a review if you like the worksheet.
Thank You
Bundle

Geometry
Geometry: This bundle includes all of the task cards listed below. Answer sheets and answer keys are provided for each topic.
Important: All these Task Cards sell for $31; as a bundle they are 35% off, for $19.95!
undefined
Sale

Completing Symmetrical Shapes - Geometry Worksheets
Completing Symmetrical Shapes - Geometry Worksheets
You’ll get 5 worksheets that you can use for short assessments, morning work or warm up exercises. Students will be able to easily practice geometry while having fun!
It’ll be a useful resource during your class that will boost your teaching efficiency!
Thank you for stopping by!
You can contact me with questions about this product. Thank you for all reviews, ratings and comments you leave on my profile!

Geometry
Geometry: This bundle includes all of the products listed below. Playing directions and folding Directions (with pictures) are Included.
Important: All these Cootie Catchers sell for $31; as a bundle they are 35% off, for $19.95!
Cootie Catchers Included: (16 Products):
♦ 3D Shapes
♦ Angle Pair Relationships
♦ Area
♦ Area of a Circle
♦ Area of Composite Figures
♦ Circumference of a Circle
♦ Missing Angles
♦ Perimeter
♦ Polygons
♦ Pythagorean Theorem
♦ Quadrilaterals
♦ Surface Area of Rectangular Prisms
♦ Volume and Surface Area of Cylinders
♦ Volume of Cones
♦ Volume of Rectangular Prisms
♦ Volume of Triangular Prisms

Geometry
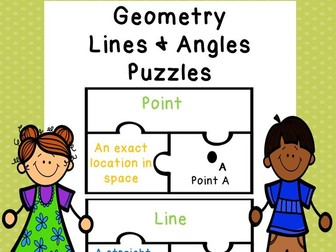
Looking for a fun interactive teaching idea for lines and angles geometry vocabulary? Well bingo! Look no further as Geometry Vocabulary for Points, Lines, Line Segments, Rays and Angles Puzzles, for CCSS 4.G.1, will serve as an exciting lesson plan for 4th grade elementary school classrooms. This is a great resource to incorporate into your unit as a guided math center rotation, review game exercise, small group work, morning work, remediation, intervention or rti. It can also be used as a quiz, drill, test, or assessment tool to help determine student mastery of the learning target. Whether a student is homeschooled or given this task as a homework assignment, kids will also love working on these for distance learning at home to study and improve their skills.
This puzzle set includes 14 colorful jigsaw puzzles. These come as pdf printable sheets that can be printed on card stock and laminated for long-term use. As a suggestion, store them in a sealable gallon storage bag and place them in a foldable bin or tub for students to use throughout the year for enrichment when they finish early. Another idea, for a craft project, is students can glue the completed puzzles into a spiral notebook or journal as a model reference sheet. They can also be glued on a poster for displaying on a bulletin board or as a wall anchor chart.
For these puzzles, students will match the geometry term with its definition and picture. By solving the problems to sort, scoot and match the puzzle pieces, students can gain confidence in an important and sometimes challenging skill. Your 4th graders will love to practice and develop strategies to learn the geometry vocab words!
I hope you download and enjoy this engaging hands-on manipulative activity with your students! So set those worksheets aside and give our puzzles a try!
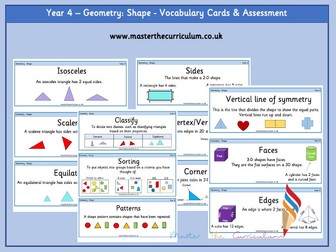
The following geometry terms are included:
Point
Line
Line Segment
Types of Lines
Intersecting Lines
Ray
Parallel Lines
Perpendicular Lines
Angles
Acute Angles
Obtuse Angles
Right Angles
Vertex
Polygons
Relevant Grade 4 Common Core Standard 4.G.A.1
Cross Reference: Texas TEKS 4.6A and Virginia SOL 4.10

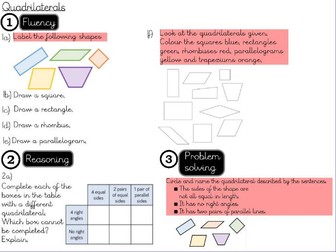
Geometry- Quadrilaterals
This is a whole lesson based on the unit of Geometry and this lesson focuses on the objective of “Quadrilaterals” This resource is tailored for year 4 and includes the teacher input ( learning journey) , independent worksheet for all chn to complete and a depth activity to deepen the children’s understanding of the concept being learned.
This document is useful for teachers who have adapted Mastery Maths or Singaporean Maths and need guidance in the approach or those who are looking for variation in fluency, reasoning and problem solving or simply those who don’t want to plan it themselves but want high quality resources and quality first teaching. =)
All of the documents that are uploaded as an Activinspire file are interactive and all of the concrete/pictorial manipulative can be used, moved and manipulated.
This document can be downloaded on Activinspire and it is also available as a PDF for those who do not have Activinspire.
Thank you for taking the time to review my resources. =)
I hope this helps you with your teaching and if it does please could you be kind enough to leave some positive feedback. =)
Kind regards,
@MasteryMaths01

Geometry
A series of printable sheets for Years 1-6.
User-friendly and student-led tasks centered on sorting, drawing and naming geometric shapes.

Geometry Math Back to School Project plus Problem Solving Tasks
This project based learning resource is an engaging Geometry based Math mini project revolving around designing a Gnome village or town using isometric paper and is a great back to school or end of term activity. The project lasts up to 5 lessons plus there are additional problem solving worksheets that could fill 2 more lessons. Includes fun geometric tasks, bursting with mathematical concepts and math skills such as isometric drawings, 3D shapes, elevation drawings and plans. It also offers opportunities to be creative and to develop number problem solving strategies.
I’m certain you and your students will enjoy Gnome Homes. My students always love it and still talk about it years later!
The aim of the task is to create all the 15 different shapes out of 4 Multilink cubes and then design a Gnomes village using these shapes as buildings. The village/town must be decorated in a theme and as this can be set as a competition within the class or year group, the student with the most creative Gnome Homes, wins.
Not only must students design their village, they must also work out the costs involved with each building relating to the ground rent, paint for the walls and tiles for the roofs.
There are activities and problem solving questions based on the task, that are available for students who need extension work.
Finished products can be laminated for a super wall display.
Can be set as a class or year group competition and entries displayed.
What’s Included
Teacher Guide
Starter activity
Printable Isometric Paper
Examples of previous work
Student worksheets
Problem Solving Tasks
Answer Keys
**Here’s what others say **
“Students completed this at the end of the year and loved it. The directions were really clear and I love the built in differentiation. One of their favorite activities of the year!”
“My students’ creativity really came through with this activity. I had gnome villages with everything from carnivals to an IKEA store. The real-world connection of costs of building was great.”
“This was a super fun project for my enriched students. They were engaged and practicing without even realizing they were.”
“Amazing resource!”

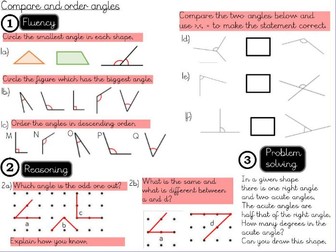
Geometry- Compare and order angles
This is a whole lesson based on the unit of Geometry and this lesson focuses on the objective of “Compare and order angles” This resource is tailored for year 4 and includes the teacher input ( learning journey) , independent worksheet for all chn to complete and a depth activity to deepen the children’s understanding of the concept being learned.
This document is useful for teachers who have adapted Mastery Maths or Singaporean Maths and need guidance in the approach or those who are looking for variation in fluency, reasoning and problem solving or simply those who don’t want to plan it themselves but want high quality resources and quality first teaching. =)
All of the documents that are uploaded as an Activinspire file are interactive and all of the concrete/pictorial manipulative can be used, moved and manipulated.
This document can be downloaded on Activinspire and it is also available as a PDF for those who do not have Activinspire.
Thank you for taking the time to review my resources. =)
I hope this helps you with your teaching and if it does please could you be kind enough to leave some positive feedback. =)
Kind regards,
@MasteryMaths01

VOLUME of cubes and cuboids - GEOMETRY - WITH ANSWERS
Excellent resource differentiated with 6 levels of differentiation on volume of cubes and cuboids, working out the volume, working backwards to find missing lengths, and using one shape to find the value of another shape.
I have used this with a set 1 and also with a nurture group using the first few level tasks to build confidence.
Can be used for any set as it has questions for the lower ability and the higher levels can stretch the higher ability.
Please do leave a review if you like the worksheet.
Thank You

Transformational Geometry
Full lesson on Transformational Geometry including:
Translations
Axial Symmetry
Axis of Symmetry
Central Symmetry
Rotation
Worksheet containing exam style questions also included.

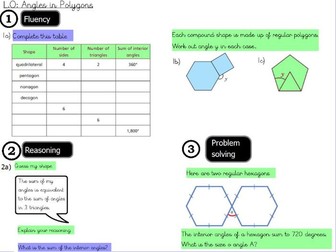
Geometry- Angles in polygons- Year 6
This is a whole lesson based on the Year 6 Geometry objective of '’Angles in Polygons". This resource includes the teacher input ( learning journey), independent worksheet and a depth activity to deepen the children’s understanding of the concept being learned.
The questions have been inspired and adapted from the White Rose Small Steps Guidance and Teaching for Mastery documents. This document is useful for teachers who have adapted Maths Mastery and need guidance in the approach or those who are looking for variation in fluency, reasoning and problem solving or simply those who don’t want to plan it themselves but want high quality resources and quality first teaching. =)
All of the documents that are uploaded as an Activinspire file are interactive and all of the concrete/pictorial manipulative can be used, moved and manipulated.
This document can be downloaded on Activinspire and it is also available as a PDF for those who do not have Activinspire.
**Please note - these resources are not compatible with Smart Notebook and the PDF file is not interactive.
**
Thank you for taking the time to review my resources. =)
I hope this helps you with your teaching and if it does please could you be kind enough to leave some positive feedback. =)
Kind regards,
@MasteryMaths01

11+ Math Practice : Geometry
Practice and revision exercises and solutions for grammar schools and independent schools entrance exams. The topics covered include:
Identify and classify the dimensions and properties of 2-D Shapes.
Identify and classify the dimensions and properties of 3-D Shapes.
Calculate the angles in Triangles, Quadrilaterals.
Classify Shapes based on their dimensions such as Isosceles, Scalene, and Equilateral Triangles.
Classify Shapes based on the angles formed by their joints such as acute, right, and obtuse angles.
Calculate unknown angles in triangles and quadrilaterals.
Calculate the area and perimeter of quadrilaterals.
Calculate the area and circumference of circles.
Calculate the volume of shapes: cuboid, sphere, cone, cylinder, tetrahedron.
Coordinates and Map: identify locations on a coordinate plane.
Transformations: reflection, enlargement, rotation
Loads of free resources in our free apps:
We provide various formats of practice exercises, quizzes, and educational games, which will prove useful to students and their parents / teachers / supporters.
Download our free Android app in the app store
Maths Quiz - Learn and Test Free & Offline
-Please note that our IOS app is currently unavailable.
.
Bundle

AQA Further Maths Level 2 - Coordinate Geometry
Covers all of coordinate geometry (unit 3) in AQA Further Maths Level 2. Lessons included are:
Linear Graphs
Equation of a Straight Line
Divide a Line in a Given Ratio
Equation of a Circle
Circles & Tangents
Bundle

Geometry Bundle
Includes a variety of geometry resources, from angles and loci to vectors and trigonometry.
Please see each individual resource for more information