AQA L2 Further Mathematics quadratics practice

What’s inside

Section 1 — Product & Sum (10 Qs)
Factor pairs → sum pair → final brackets. ✔ / ✖ feedback.
Section 2 — Completing the Square (10 Qs)
Fill (x+h)2+k(x+h)^2+k(x+h)2+k and, when possible, factor the difference of squares.
Section 3 — Factorising with a≠1a\neq1a=1 (10 Qs)
AC‑method scaffold: factor pairs of acacac, sum to bbb, final (ax+p)(cx+q)(ax+p)(cx+q)(ax+p)(cx+q).
Section 4 — Factorise by Completing the Square (a ≠ 1) (10 Qs)
Fill ((2ax+b)2−D2)/(4a)\big((2ax+b)^2 - D^2\big)/(4a)((2ax+b)2−D2)/(4a) then final factorisation.
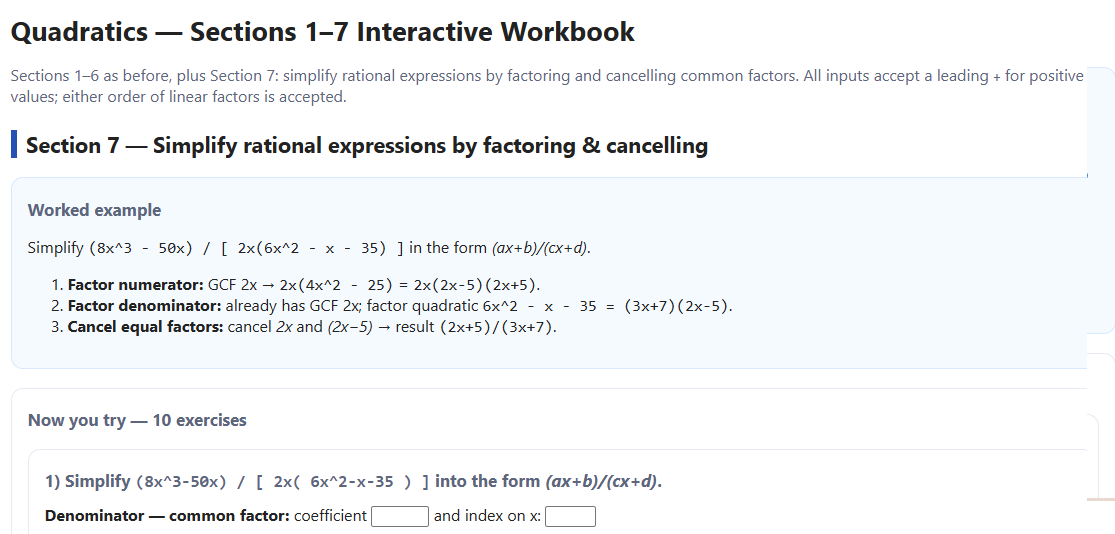
Unified styling, instant marking, accepts + for positives and either bracket order.What Section 5 includes

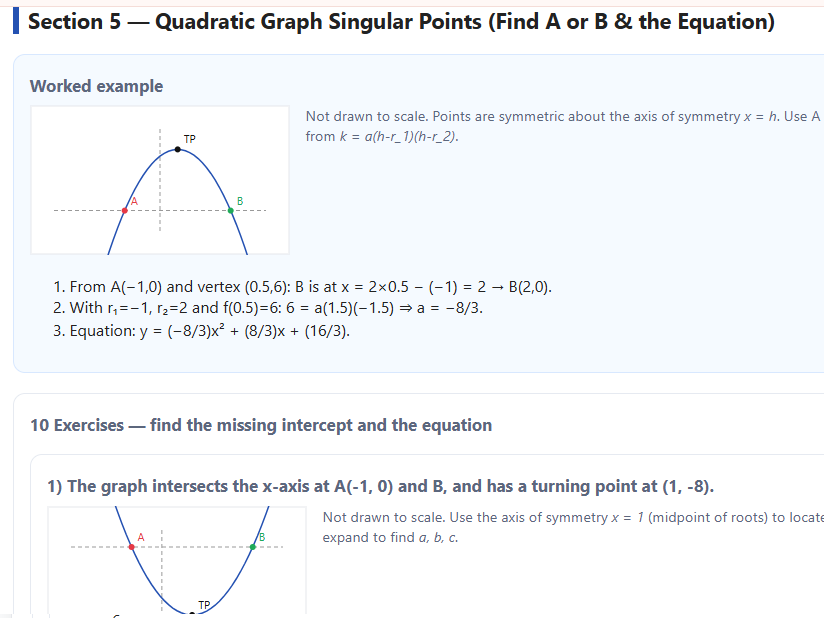
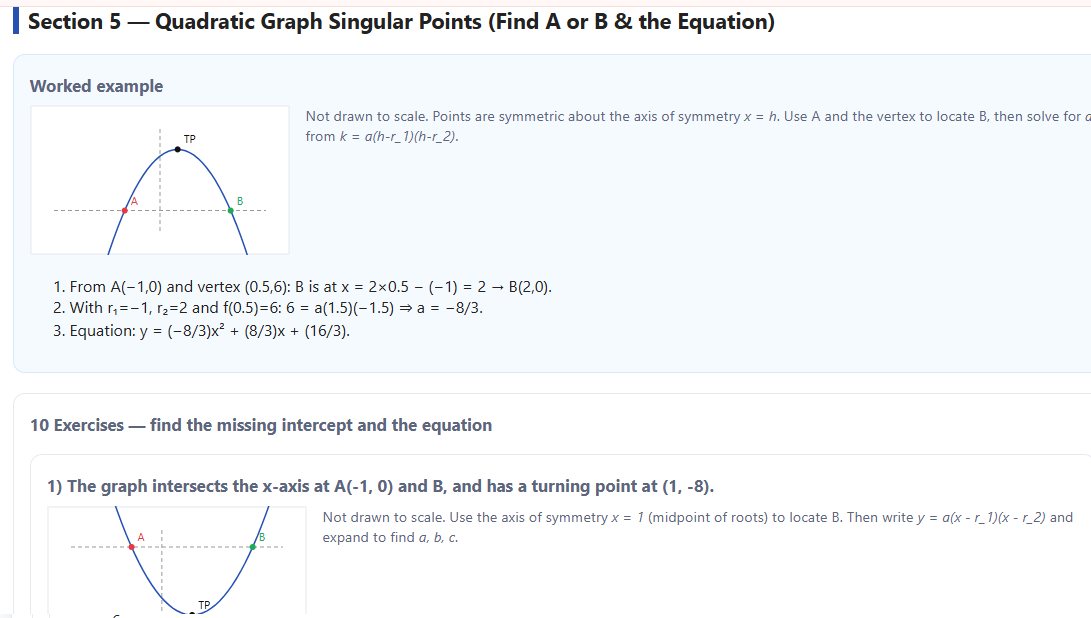
Worked example (matches your screenshot’s style):
Given A(−1,0)A(-1,0)A(−1,0) and turning point (0.5,6)(0.5, 6)(0.5,6), it finds B(2,0)B(2,0)B(2,0).
Then it determines aaa from k=a(h−r1)(h−r2)k=a(h-r_1)(h-r_2)k=a(h−r1​)(h−r2​) and expands to the standard form.
10 exercises with integer-friendly coefficients:
Each card displays the known intercept (either AAA or BBB) and the turning point.
Students fill:

The missing point ( , __ )(,__,,__,)(,__) — the y‑coordinate must be 0.
The equation y=_ x2+_ x+_y = _,x^2 + _,x + _y=_x2+x+.
Answers accept + for positive entries; ticks turn on when correct; same green/red marking as your other sections.What Section 6 teaches

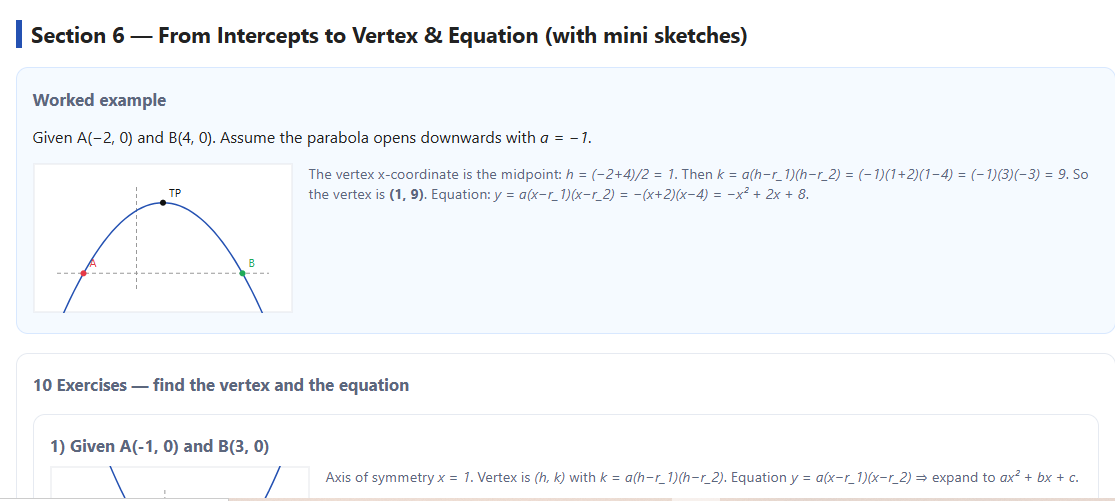
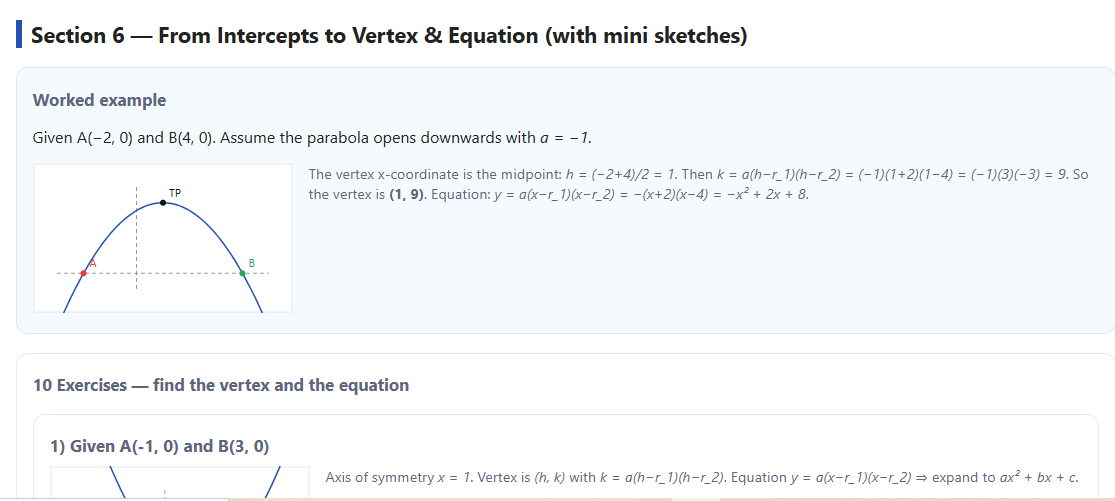
Vertex from intercepts: h=r1+r22h = \dfrac{r_1 + r_2}{2}h=2r1​+r2​​ (axis of symmetry), and k=a(h−r1)(h−r2)k = a(h-r_1)(h-r_2)k=a(h−r1​)(h−r2​).
Equation from intercepts: y=a(x−r1)(x−r2)y = a(x-r_1)(x-r_2)y=a(x−r1​)(x−r2​) → expand to ax2+bx+cax^2 + bx + cax2+bx+c, with
b=−a(r1+r2)b = -a(r_1+r_2)b=−a(r1​+r2​), c=a(r1r2)c = a(r_1r_2)c=a(r1​r2​).
Inputs are auto‑checked with ✔/✖; numbers can be integers or decimals (e.g. 1.5, 9, −4.5).
The SVG thumbnails are not to scale but do show opening direction and the relative placement of A, B, and the turning point.