Complete no-prep lesson with 50+ slides tasks, answers and unique exam questions, on Transformers and the National Grid for the Electromagnetism Topic of GCSE (9-1) Science / Physics. Please note, if you are looking for the National Grid lesson for the Electricity Topic it is here: https://www.tes.com/teaching-resource/resource-12668952 As a Secondary Science teacher and Deputy Headteacher for many years I make high quality no-prep lessons so busy teachers can teach outstanding lessons without spending hours planning. This high quality lesson includes explanations, different types of in-lesson assessment (all with answers) and unique exam questions. My lessons are ideal for non-Physicists because I myself retrained as a Physics teacher despite having a background in Biology. Having to learn the subject myself means I know how to take learners on a journey that builds up their understanding step by step, while still going into a lot of depth. The preview video shows a representative sample of slides from the resource so that you get a good idea of what it includes before you buy. What’s Included: Two starters so you can extend this over two lessons if needs be. Explanation slides in “chunked” sections with animated diagrams. Worked examples of calculations. Editable diagrams and animations which help aid understanding. Multiple questions in different question styles and difficulties - no need for worksheets. Most “chunked” explanation sections include a set of “learning check quick questions” followed by a set of in-depth questions on the learning from that “chunk” of the lesson. Exam-style questions on the whole lesson at the end of the lesson- these are uniquebased on real exam questions but not just copied from exam boards. Answers for all questions All easily editable to adapt to your teaching or to use in existing lessons. Slightly humourous, at points, if you like that sort of thing. 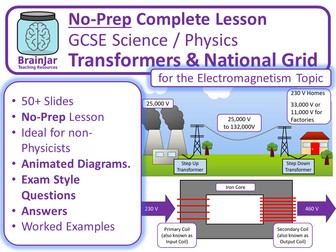Learning objectives: Describe what a transformer does, and its structure. Explain how transformers work, including how the ratio of potential differences relates to the ratio of turns on each coil. Explain how an alternating current in the primary coil induces an alternating potential difference in the secondary coil. Apply the following equations: Vp / Vs = Np / Ns and V s × Is = V p × I p Use the equations to describe the advantages of power transmission at high potential differences. The lesson was written for AQA GCSE Physics but is very likely to be applicable to other exam specifications. Please leave a rating / review and all other feedback gratefully received!

Transformations Pack: Students must reflect, rotate and translate different shapes to reveal the secret pictures! Pack contains: Translations Mystery Picture Suitable for younger students just learning translations and vectors. Reflections Mystery Pictures 1 & 2 Also suitable for younger students just starting to learn about reflections in a mirror line. The second version uses the co-ordinates axes and the line y = -x as mirror lines. Rotations Mystery Pictures 1 & 2 Students will need to be able to rotate 90 degrees and 180 degrees about a point. Most students will need tracing paper. The first version is on the co-ordinate plane and all rotations are about the origin. Mixed Transformations Pictures 1 & 2 These activities require students to use translations, reflections and rotations. Combined Transformations Pictures 1 & 2 These are the most difficult pictures to complete and require students to do multiple transformations to each object in order to find its place. The second picture takes place on the co-ordinate plane. Answers are included and can be checked at a glance, making it easy for students and teachers to know whether things are on track!

A powerpoint on all four transformations - Translations, reflections, rotations and enlargements. Suitable for years 8-11 preparing for the GCSE Maths exams. There are a few questions to test knowledge as well as step by step guides on how to do each transformation. Leave a good review for more good quality resources. Suitable for a lesson. Enjoy :)

A timeline revision activity for A Christmas Carol that asks students to offer 3 layers of analysis for 13 key Scrooge quotations to help track his transformation in the novel from a solitary miser to a redeemed philanthropist. A01: What is the meaning of the quotation? A02: What is the impact of words/methods? A03: What is Dickens’ message in this quotation? Comprehensive answer sheet is included. I give this out at the end of the lesson so students can compare their answers to it. Ideal revision activity in the run up to the May examinations.

The main part of this PowerPoint is 30 slides, it begins with the calculation and shape of the three Trig graphs, then introduces the four ways in which the graphs can be transformed f(x) = A sin B(x+C)+D. Each of the transformations are considered individually with examples, then each has three “state the function” questions for students to answer verbally (slides 14, 18 ,23, 27). Next, an example of a function with all four transformations is worked with steps in appropriate order. The main part of the slide show concludes with another statement of the “four-transformation form of equation”, and an example of the four resultant transformations are shown step by step. Slides 32 -34 are graph drawing worksheets with answers appearing, for which masters are included as word documents since you may wish to use these for students practice work. Slide 35 is a table to complete with values for the given formulas each with 2 transformations, and slide 36 shows the 3 standard Excel drawn graphs.

Basics of how to carry out translations, reflections and enlargements. Examples with and without coordinate axes. Rotations not included as I used applets for that.

Success criteria- State the basic structure of a transformer. Describe how a transformer works. Explain the difference between a step-up and step-down transformer. Use the transformer equation.

Introducing the Transformation of Matrices. Examples to work through.

Save your time teaching reflections with this resource. It will help your students to understand main concepts: mirror line congruent shapes using coordinates Resource consists of: 1 animated presentation (ppsx) 1 practice worksheet 2 reveal the picture worksheets Answer keys

Reflection, Rotation, Translation, KS3 Maths Transformations

A fabulous way to look at combinations, rotations and reflections of a square. The square is coloured to show the transformations. A great resource. It is a shame this is downloaded by only 10% of viewers. (The mistake has been corrected)

Engage your pupils in practicing how to enlarge shapes by a fractional scale factor, now included at foundation tier GCSE. This task requires pupils to enlarge shapes by a given scale factor from a given point, if correctly completed it will spell out a hidden word. You'll get full instructions, answers and thoughtful ideas for extension - everything you need for a great lesson! Try one of our resources for free!

This is a whole lesson on learning how to Transform Trig Graphs and draw or name the transformation. This is the fourth lesson that I would teach on trig graphs and builds on an understanding of transforming functions, by looking at Transforming Trigonometric Graphs. This lesson is ready to go, with no prep required. It is also great for home learning. 18 slide presentation + resources. The lesson includes: a Starter (on angles and surds) learning objectives (differentiated) keywords Excellent teaching slides MWB activities Lots of examples a worksheet (with answers) a handout (rules to learn – great for student notes) Plenary Geometry: All Lessons + All Resources LASTLY: This lesson is flat packed for copyright purposes Please provide a RATING with written feedback Please email outstandingresourceshelp@gmail.com if there are any issues.

A lesson on what electrical energy is in realation to E=QC and Q=IT leading on to how it can be transformed by components

This power point on transformation clearly explains how to transform shapes using rotation, reflection and translation. I use this for my KS3 and KS4 students.

Presentation and worksheet. Suitable for GCSE/IGCSE and A level.

PowerPoint lessons for the following topic Transformations They include: Questions and answers Animated parts of the answer for Q&A and demonstrations Colours to support explanations. For your use: You can duplicate slides any type in new questions To support your teaching and save time planning As a basis for your observations lessons To share with students to help them work outside the classroom I hope this benefits you as it has done for me. Kind regards.

This well thought out booklet has been structured to increase in difficulty gradually, beginning with scaffolded intro examples and building up to more challenging questions that get them thinking.   Under the hood Reflecting shapes on a grid Rotating shapes on a grid Translating shapes on a grid Describing reflections, rotations and translations Challenge questions involving combined translations and reflecting in the lines y = x and y = -x.   Thorough, comprehensive, and carefully designed to boost confidence and grades.   Answers included Not completely convinced? Download a free preview of the sheet here. https://www.tes.com/teaching-resource/resource-12482174