Mentor4Maths's Shop
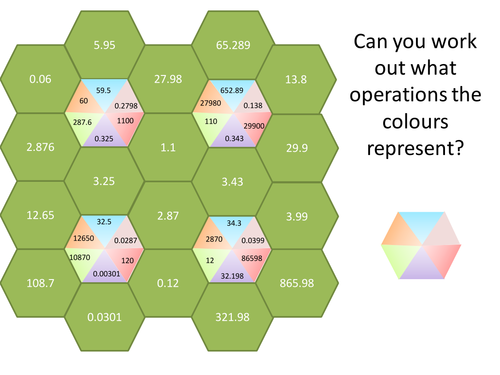
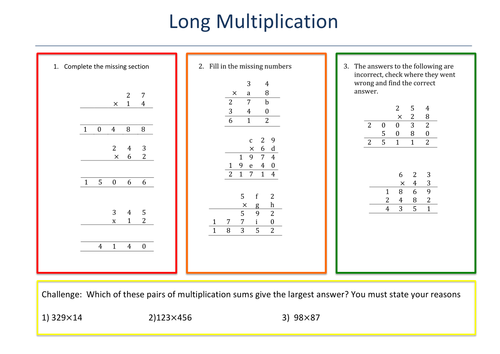
As a secondary maths teacher I enjoy making my own resources. These have either been made for school or for tuition all designed with students in mind. Resources include differentiation and focus on fluency, reasoning and problem solving.