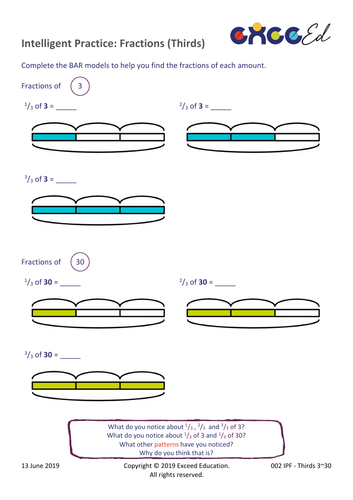
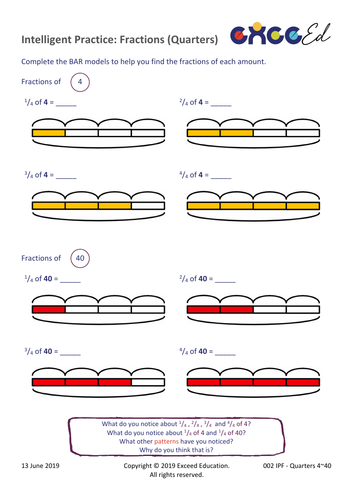
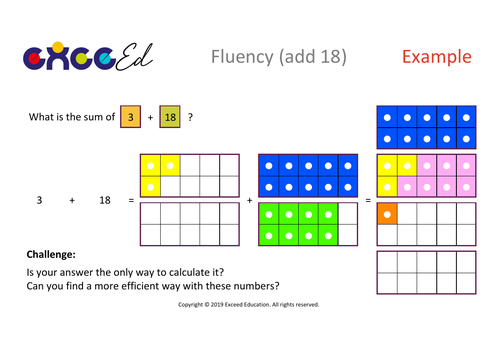
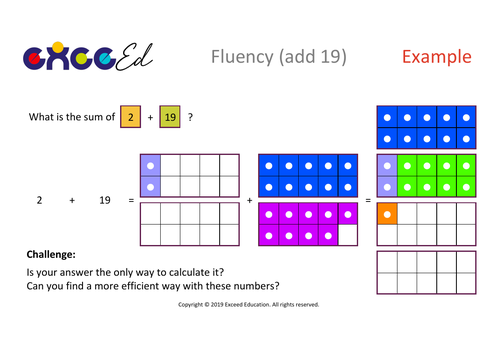
Exceed Education's Shop
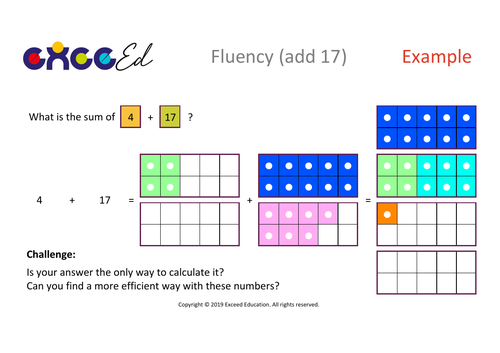
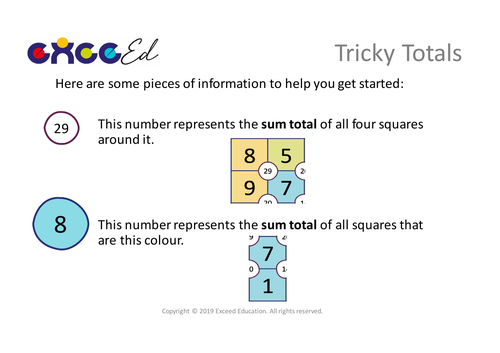
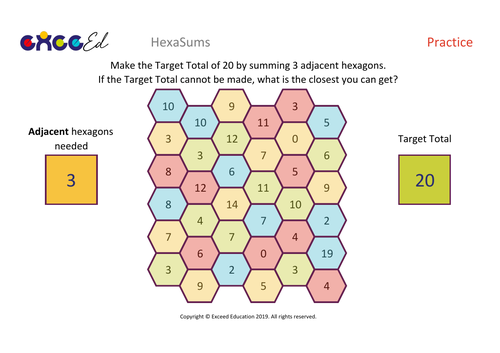
I create resources for mathematics teaching based on the Singapore and Shanghai curriculum models for best practice. I will focus on the core principles of Intelligent Practice, Low-Threshold High-Ceiling tasks, fluency based activities and Problem Solving and Reasoning activities.